Вычислите 
(Не разрешается использовать таблицы и микрокалькуляторы.)
Решение. Пусть 
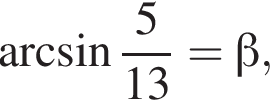
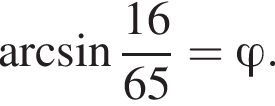Отметим, что все углы находятся в промежутке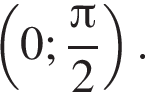 
Тогда 
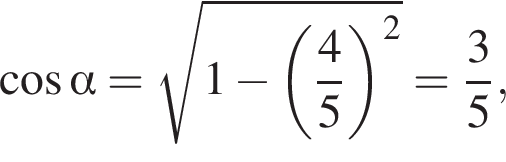
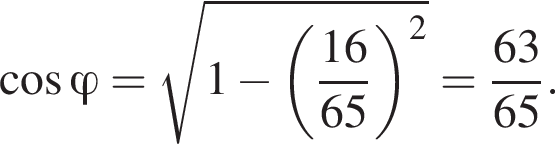
Таким образом,
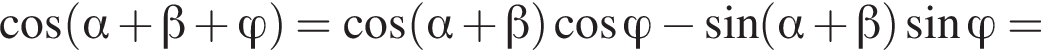
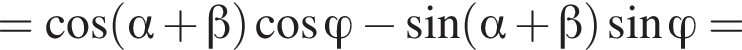
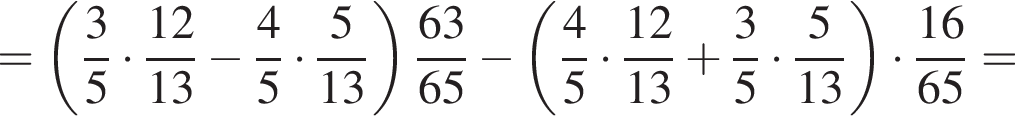
Ответ: 0.
| За задание (или за каждый из четырех пунктов сюжета из четырех заданий) выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |
в другом виде:
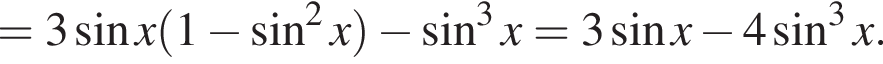
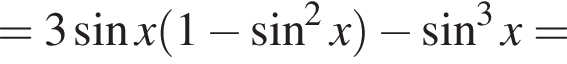
Отсюда:
и 
где 
и 
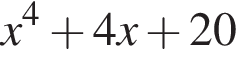положителен при всех значениях 
Действительно, его производная 
обращается в ноль только при 
Это единственная точка минимума, следовательно, значение много члена при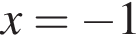 
— наименьшее, оно равно 17.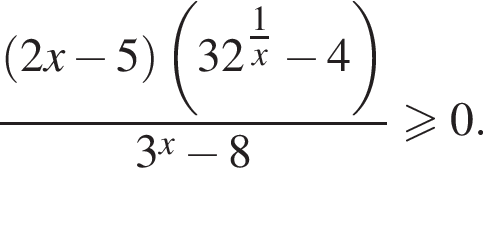
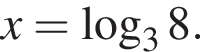и 
Обращается в ноль при 
причем эта точка кратности 2. Отметим найденные точки на числовой оси и применим метод интервалов. Так как при 
и 
и 
совпадают.
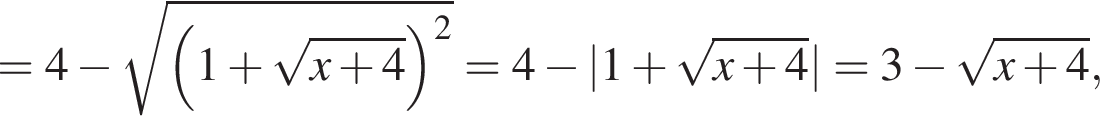
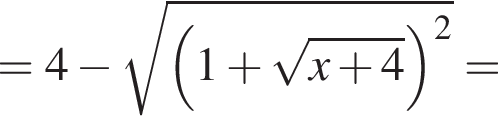
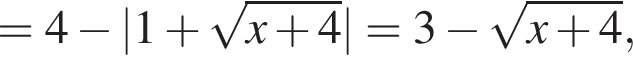
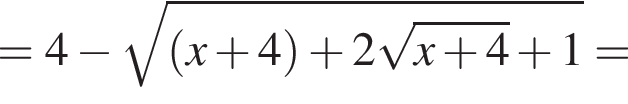
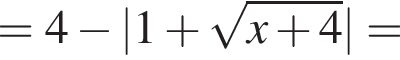
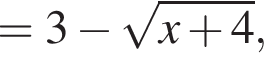
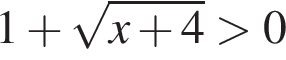при всех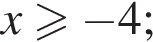 
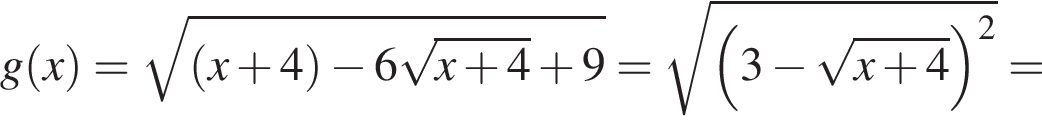
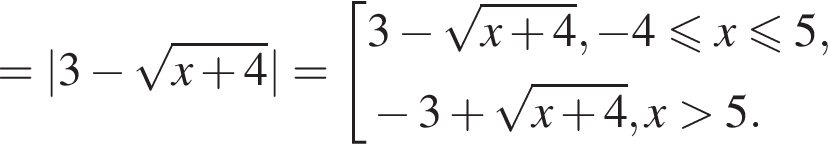
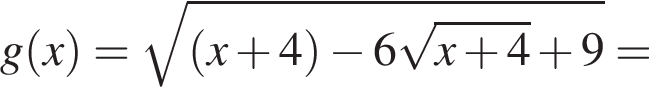
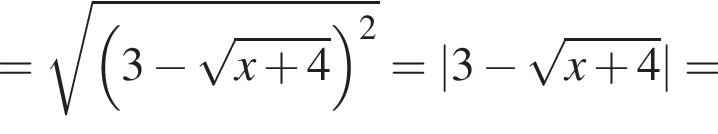
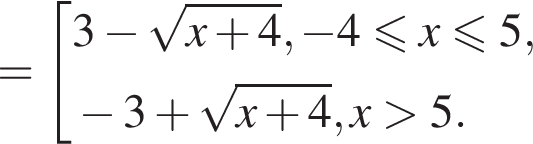
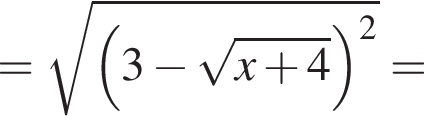
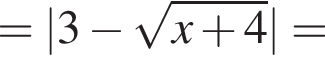
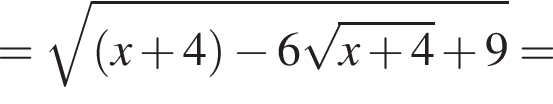
на отрезке 
на этом отрезке, следовательно, совпадают их графики. Длина отрезка 
равна 9.
(Найдите область определения, множество значений, промежутки монотонности, точки экстремума, экстремумы, промежутки выпуклости, асимптоты, нули.) Постройте ее график.
При этих значениях x она дифференцируема.
Причем, если 
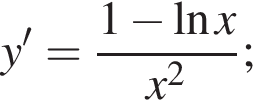
если 
если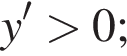 
На промежутке 
функция возрастает, так как для этих значений x 
на промежутке 
функция убывает, так как 
Точка 
— точка максимума.
— ее наибольшее значение.
если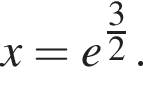 
На промежутке 
функция имеет выпуклость, так как для этих значений x 
на промежутке 
функция имеет вогнутость, так как 
Таким образом, 
— точка перегиба. значение функции в этой точке равно 
значение производной 
и 
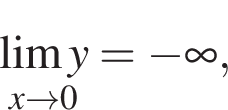то есть кривая графика функции асимптотически приближается справа к прямой 
то есть кривая функции асимптотически приближается сверху к прямой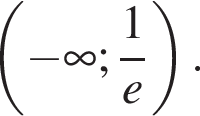 
изображен на рисунке.
проведенная в точке графика с абсциссой 1, имеет с этим графиком ровно одну общую точку.
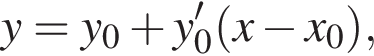где 
и 
— значения функции и ее производной при x0 = 1:
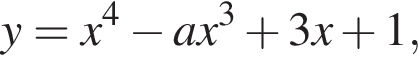
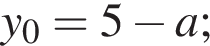
или после преобразований,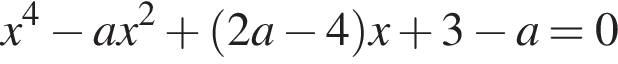 
определяет абсциссы общих точек графика функции и касательной к нему. По условию задачи это уравнение должно иметь одно действительное решение. Но так как рассматриваемое уравнение четвертой степени, это возможно лишь в двух случаях: либо когда уравнение имеет один действительный двукратный корень, либо — один четырехкратный корень. Одно решение нам известно — 
Значит, 1 — по меньшей мере — двукратный корень, и, следовательно, многочлен в левой части уравнения делится на 
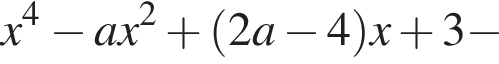
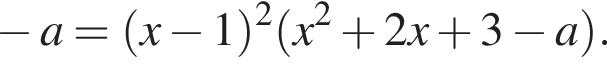
таким образом, должен иметь либо кратный корень, либо не иметь действительных корней. Эти условия выполняются, когда его дискриминант неположительное число, т. е. когда 
что возможно при 
Но если 
трехчлен 
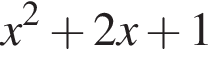имеет кратный корень -1, что нарушает условие задачи. 
имеет с касательной к нему в точке с абсциссой 1 ровно одну общую точку при всех 