2. Дана функция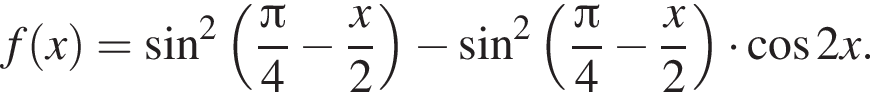 
а) Решите уравнение 
б) Вычислите 
в) Решите неравенство 
на отрезке 
г) Найдите множество значений функции 
на отрезке 
Решение. Преобразуем исходную функцию:
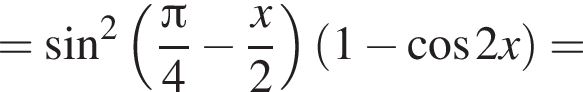
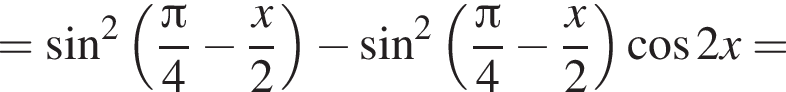
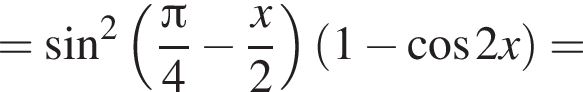
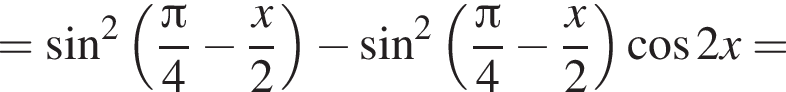
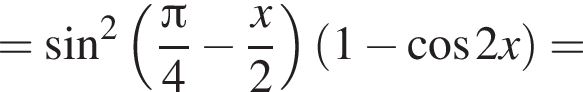
а) Запишем уравнение в виде 
откуда 
или 
то есть 
или 
б) Поскольку 
получаем
в) Обозначим 
тогда получим
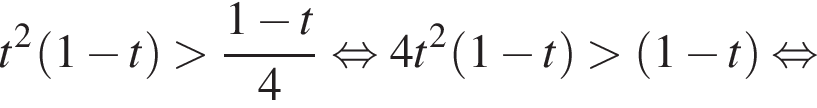
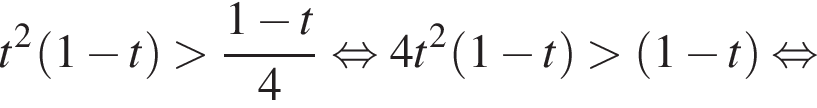
Заметим, что 
при всех 
Кроме того, 
во всех случаях, кроме тех, когда что на указанном отрезке происходит лишь при 
Следовательно множитель 
положителен всегда, а множитель 
— всегда кроме точки Сократим на эти множители. Останется неравенство 
Поскольку 
возрастает на 
и убывает на 
а кроме того 
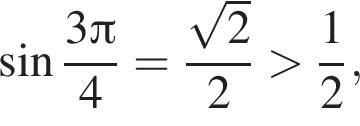в данное неравенство подходят 
Окончательный ответ 
г) При 
принимает все значения на 
Поэтому осталось определить область значений функции 
на отрезке Рассмотрим функцию 
и возьмем ее производную
и отрицательно при 
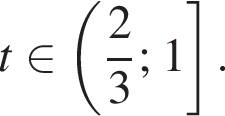Значит, 
возрастает при 
и убывает при 
При этом 
и 
(см. пункт б). Поэтому областью значений функции будет отрезок 
Ответ: а) 
б) 
в) 
г) 
| За задание (или за каждый из четырех пунктов сюжета из четырех заданий) выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |
б) в) г) б) в) г)