Найдите площадь фигуры, ограниченной графиком функции 
и касательными к нему, проходящими через точку 
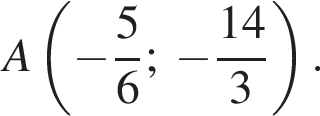
Решение. График данной функции представляет собой части двух парабол:
при 
и 
при 
Найдем касательные отдельно к каждой параболе. Любая прямая, кроме вертикальной, проходящая через точку 
может быть задана уравнением 
причем
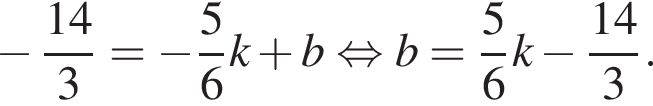
Итак, уравнение этой прямой имеет вид
При этом она имеет единственную общую точку с параболой 
То есть уравнение
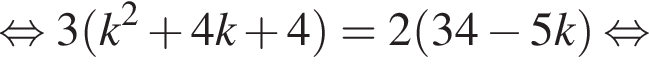
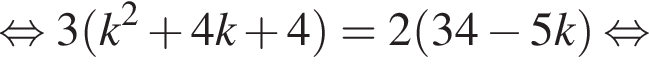
Абсциссу точки касания, тот самый единственный корень уравнения, можно найти по формуле 
В первом случае 
а во втором 
поэтому прямая касается параболы в той части, где она не представляет график исходной функции. Эта касательная в дальнейшем не нужна.
Найдем касательную к другой половине графика. Она имеет единственную общую точку с параболой 
То есть уравнение
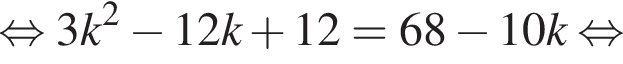
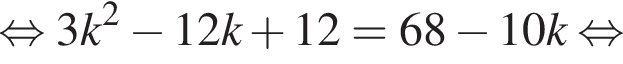
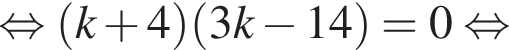
Абсциссу точки касания, тот самый единственный корень уравнения, можно найти по формуле 
В первом случае 
а во втором 
поэтому прямая касается параболы в той части, где она не представляет график исходной функции. Эта касательная в дальнейшем не нужна.
Итак, область ограничена сверху графиком исходной функции, а снизу прямыми
Эти прямые пересекают ось абсцисс в точках соответственно 
и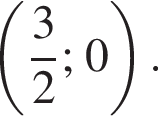 
Ниже оси, следовательно, расположен треугольник высотой 
и основанием 
поэтому его площадь составляет
Опустим перпендикуляры на ось абсцисс из точек 
и 
К фигуре пристроятся прямоугольные треугольники площадью
Теперь осталось только найти площадь под графиком исходной функции, вычесть добавленную площадь и прибавить площадь нижнего треугольника
Ответ: 
| За задание (или за каждый из четырех пунктов сюжета из четырех заданий) выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |