Через точку A(−3; 1) проведена прямая, которая является касательной к графику функции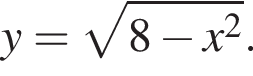 
Определите угол наклона этой прямой к оси абсцисс. Сделайте рисунок с изображением графика данной функции и данной касательной.
Решение. Уравнение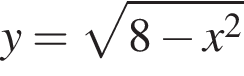 
или 
при условии y ⩾ 0, задает полуокружность с центром в начале координат и радиусом 
Допустим, что уравнение касательной имеет вид 
тогда 
(условие прохождения через точку (−3; 1)) и расстояние от начала координат до прямой 
равно радиусу окружности, то есть 
Из первого уравнения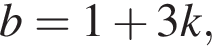 
тогда из второго:
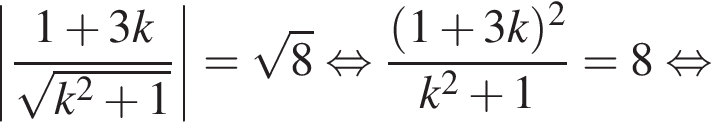
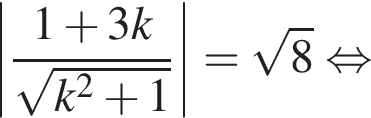
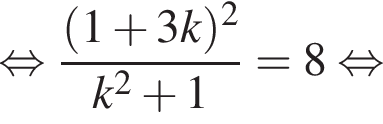
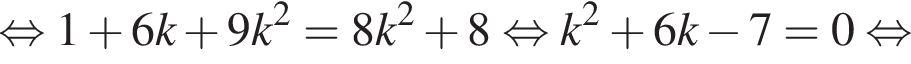
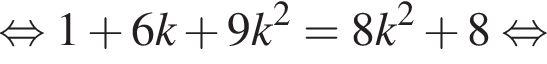
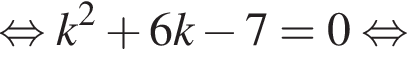
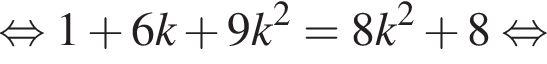
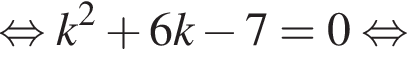
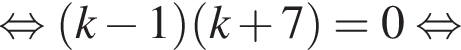
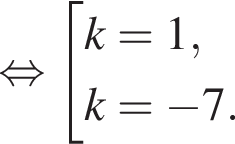
Отсюда b = 4 или b = −20.
Итак, уравнения касательных к этой окружности имеют вид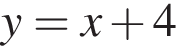 
и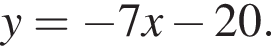 
Однако вторая касательная касается нижней половины окружности и нам не подходит. Первая же имеет угловой коэффициент 1, поэтому образуем с горизонтальной осью угол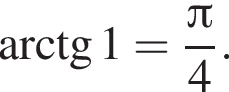 
Ответ: 
II способ.
Поскольку искомая касательная проходит через точку A(−3; 1), её уравнение имеет вид
Рассмотрим систему
и перейдём от неё к уравнению
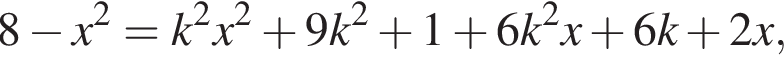
которое можно записать иначе:
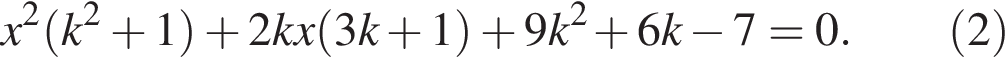
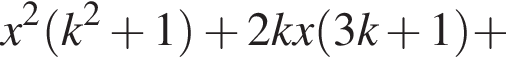
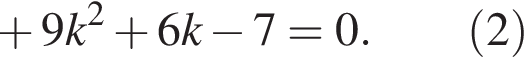
Прямая 
будет касательной к графику данной функции, если уравнение (2) будет иметь один корень, т. е. его дискриминант окажется равным нулю:
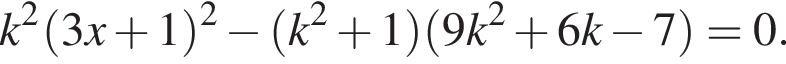
Отсюда k1 = 1, k2 = −7. Проверка показывает, что при k = 1 система (1) имеет одно решение, при k = −7 не имеет решений.
III способ.
Пусть FM — касательная к окружности 
(см. рис.). Тогда прямая FM перпендикулярна прямой OM. Из треугольника OAM имеем:
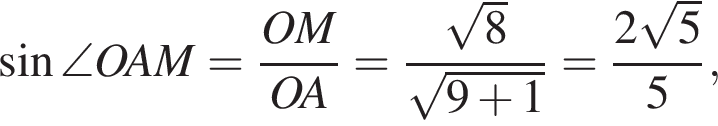
а 
Проведём прямую AP перпендикулярно FO. Из треугольника OAP:
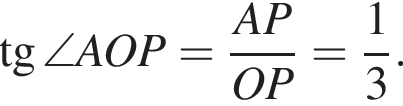
Угол MAO является внешним углом для треугольника OAF, тогда 
Значит,
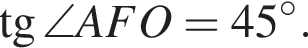
IV способ.
Из условия следует, что 
OP = 3, AP = 1. По теореме Пифагора из треугольников APO и AMO находим 
Положим AF = x, FP = y. Поскольку треугольники FMO и FPA подобны, получим:
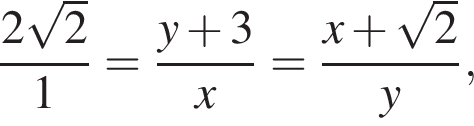
откуда
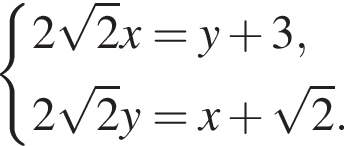
Из системы уравнений находим, что 
и заключаем: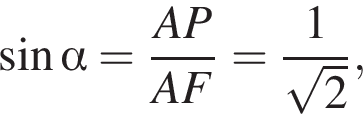 
т. е. α = 45°.
| За задание (или за каждый из четырех пунктов сюжета из четырех заданий) выставляется одна из следующих оценок: + (3 балла), ± (2 балла), ∓ (1 балл), − (0 баллов) При этом необходимо руководствоваться следующим. | |
| Критерии оценивания выполнения заданий | Баллы |
|---|---|
| Верное и полное выполнение задания | 3 |
| Ход решения верный, решение доведено до ответа, но допущен один недочет | 2 |
| Ход решения верный, решение доведено до ответа, но допущено два недочета или одна грубая ошибка | 1 |
| Остальные случаи | 0 |
| К недочетам относятся, например: описки, неточности в использовании математической символики; погрешности на рисунках, недостаточно полные обоснования; неточности в логике рассуждений при сравнении чисел, доказательстве тождеств или неравенств; вычислительные ошибки, не повлиявшие принципиально на ход решения и не упростившие задачу, если задача не являлась вычислительной; замена строго знака неравенства нестрогим или наоборот; неверное присоединение либо исключение граничной точки из промежутка монотонности и аналогичные. Грубыми ошибками являются, например: потеря или приобретение постороннего корня; неверный отбор решения на промежутке при правильном решении в общем виде; вычислительная ошибка в задаче на вычисление; неверное изменение знака неравенства при умножении на отрицательное число, логарифмировании или потенцировании и т. п. | |